Unsur-Unsur Tabung dan Rumusnya - Pasti kita sering menjumpai bentuk kaleng susu dengan sisi bawah dan sisi atas berbentuk lingkaran. Nah, kaleng susu tersebut adalah salah satu contoh benda berbentuk tabung. Lalu, apa itu bentuk tabung? Simak ulasan berikut di bawah ini tentang pengertian dan unsur-unsur tabung dan rumusnya.
Tabung merupakan bangun ruang tiga dimensi yang dibatasi oleh unsur pembentuknya, yaitu sisi alas dan sisi atas berbentuk lingkaran yang kongruen dan sejajar, serta sisi lengkung yang disebut sebagai selimut tabung.
Unsur-unsur pada tabung tersebut sangat penting untuk dipelajari karena merupakan dasar-dasar perhitungan pada tabung. Selain itu, dengan mengenal unsur dan bagian tabung, kita dapat dengan menentukan ciri dan sifat bangun ruang tabung. Adapun ciri-ciri dan sifat tabung, antara lain:
- Tabung memiliki 3 buah sisi, yaitu 2 buah sisi datar berbentuk lingkaran kongruen dan 1 buah sisi tegak berupa lengkungan persegi panjang.
- Tabung memiliki 2 rusuk, yaitu 1 buah rusuk pada sisi alas dan 1 buah rusuk pada sisi atas.
- Tabung tidak memiliki titik sudut.
Unsur-Unsur Tabung
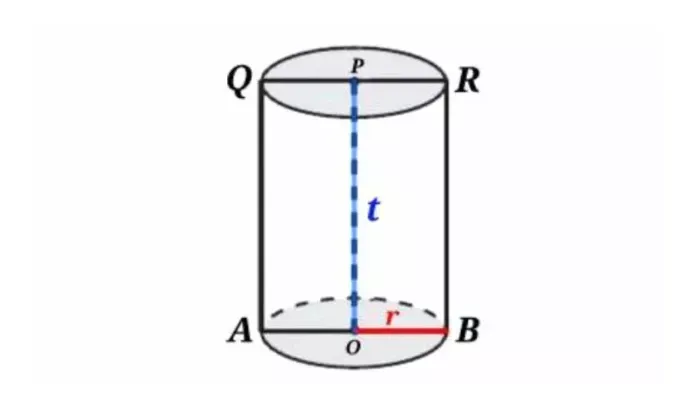
Agar bisa dengan mudah dalam mengenal dan memahami unsur-unsur pembentuk tabung, perhatikan gambar contoh bangun ruang tabung di atas.
1. Sisi Alas dan Atap Tabung
Bagian-bagian tabung yang pertama ada sisi alas dan tutup tabung. Seperti yang sudah disinggung sebelumnya, bahwa tabung dibatasi oleh dua buah lingkaran. Lingkaran pada bagian bawah disebut sisi alas dan lingkaran pada bagian atas disebut dengan tutup tabung.
Pada contoh gambar tabung di atas, sisi alas tabung ditujunkan oleh lingkaran dengan pusat O, sedangkan atap atau tutup tabung ditunjukan oleh lingkaran dengan pusat P. Adapun unsur-unsur pembentuk lingkaran, antara lain:
a. Pusat Lingkaran
Pusat lingkaran merupakan titik tengah yang mempunyai jarak sama terhadap himpunan titik-titik tepi lingkaran. Perhatikan contoh gambar tabung di atas, pusat lingkaran pada sisi bawah (titik O) dan pusat lingkaran pada sisi atas (titik P) merupakan pusat lingkaran tabung.
b. Jari-Jari Lingkaran (r)
Jari-jari lingkaran merupakan jarak pusat lingkaran ke himpunan titik-titik tepi lingkaran. Coba perhatikan gambar tabung di atas, jari-jari lingkaran ditunjukan oleh jarak dari titik O ke titik A atau jarak dari titik O ke titik B. Sementara itu, jari-jari lingkaran pada tutup tabung ditunjukan oleh jarak dari titik P ke titik Q atau jarak dari titik P ke titik R.
c. Diameter Lingkaran (d)
Diameter lingkaran merupakan jarak antara titik-titik himpunan lingkaran yang melewati titik pusat. Dengan kata lain, diameter adalah dua kali jari-jari lingkaran. Perhatikanlah contoh tabung di atas, diameter lingkaran pada sisi alas tabung ditunjukan oleh garis AB. Sedangkan diameter lingkaran pada tutup tabung ditunjukan oleh garis QR.
Sisi alas dan sisi tabung dapat kita hitung luasnya menggunakan rumus lingkaran, yaitu sebagai berikut:
Luas Lingkaran = π × r²
2. Tinggi Tabung
Tinggi tabung merupakan jarak antara titik pusat lingkaran sisi alas dengan titik pusat lingkaran tutup tabung. Coba lihatlah gambar tabung di atas, tinggi tabung ditunjukan oleh garis t yang merupakan jarak dari titik O ke titik P.
3. Selimut Tabung
Selimut tabung merupakan sisi tegak berupa lengkungan pada tabung yang menghubungkan sisi atas dan sisi atas tabung. Jika sebuah tabung dibongkar, maka selimut tabung mempunyai bentuk persegi panjang. Sehingga, selimut tabung dapat kita hitung luasnya menggunakan rumus keliling lingkaran dikali tinggi tabung.
Luas Selimut Tabung = Keliling Lingkaran × Tinggi Tabung
Luas Selimut Tabung = 2 × π × r × t
Rumus-Rumus Tabung
Setelah mempelajari unsur-unsur bangun ruang tabung, maka diperoleh kesimpulan bahwa untuk menghitung luas dan volume tabung dapat menggunakan rumus di bawah ini.
Rumus Luas Tabung = (2 × Luas Lingkaran) + (Luas Selimut Tabung)
Rumus Luas Tabung = (2 × π × r²) + (2 × π × r × t)
Rumus Volume Tabung = Luas Alas × Tinggi
Rumus Volume Tabung = π × r² × t
Demikianlah pembahasan lengkap mengenai unsur-unsur tabung dan rumusnya. Semoga penjelasan di atas mudah untuk dipahami dan dapat bermanfaat bagi kita semua.